Binary To Hexadecimal Converter

2
16

Converting steps:

How to convert binary to hexadecimal?

Converting binary to hexadecimal is really fun. Converting binary to hexadecimal involves grouping binary digits into sets of four, finding the hexadecimal equivalent for each group, and combining the results to get the final hexadecimal representation. It is based on the fact that 24 = 16 allowing the direct mapping of four binary digits to one hexadecimal digit. Here is an example below:

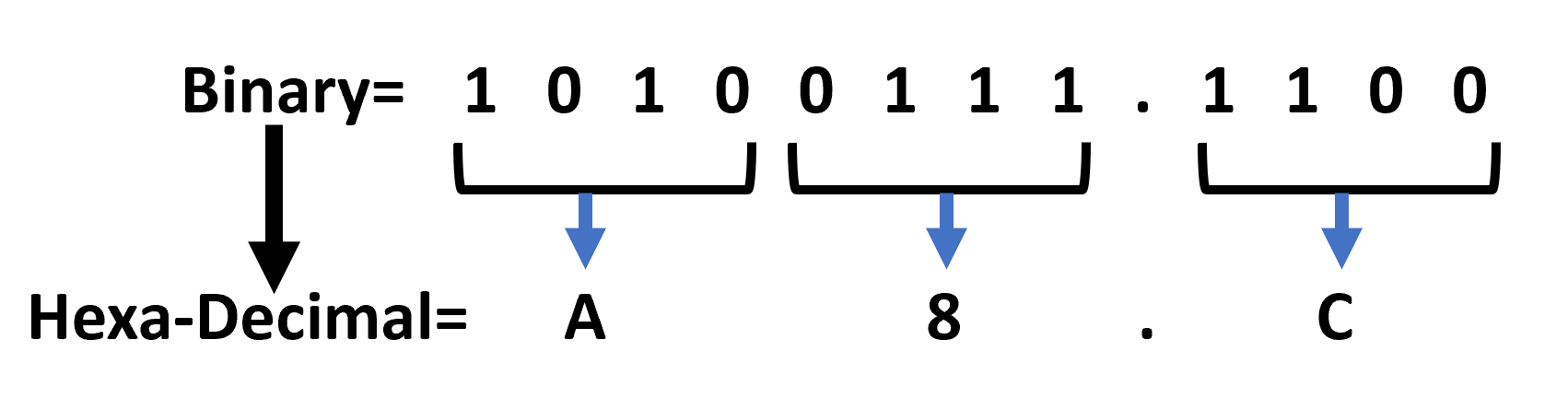
Binary to Hexadecimal Conversion

An example of binary number to hexadecimal number conversion:


(1111010.1001111)2 = (?)16 or make a conversion binary to hexadecimal.

Binary= 1 0 1 0 0 1 1 1 . 1 0 0 1 1 1 1 0
Chunk= ________ ________ . ________ ________
Arrows= ↓ ↓   ↓ ↓
Hexadecimal= A 7 . 9 E

Result is: (A7.9E)16

[N:B: Take only 4 binary digit to make hexadecimal. If you do not have enough binary digit to make 4 digit before floating point then add extra 0 in the most left side before floating point and if you need to make 4 digit after floating point then add a extra 0 in the most right side after floating point, as like example.]

Binary to Hexadecimal conversion table:

Binary Hexadecimal
0 0
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F