Hexadecimal To Decimal Converter
How to convert a hexadecimal number to the decimal number?
To convert a hexadecimal number to decimal, it is crucial to understand the positional value of each digit. Begin by assigning decimal values to the hexadecimal digits: 0-9 retain their values, while A=10, B=11, C=12, D=13, E=14, and F=15. Starting from the rightmost digit, multiply each digit by 16 raised to the power of its position (counting from right to left, starting with 0). Sum up these values to obtain the decimal equivalent. Strongly emphasize the importance of correct digit placement and the exponential relationship with the base (16) for accurate conversion.
For dn number of hexadecimal digit.[where n is positon of that digit.]:
dn-1 .... d4 d3 d3 d2 d1 d0 . d-1 d-2 d-3
The decimal number is equal to the sum of hexadecimal digits (dn) times their power of (16n):
decimal = dn-1 x 16n-1 + .... + d1 x 161 + d0 x 160 + d-1 x 16-1 + .... + d-n x 16-n
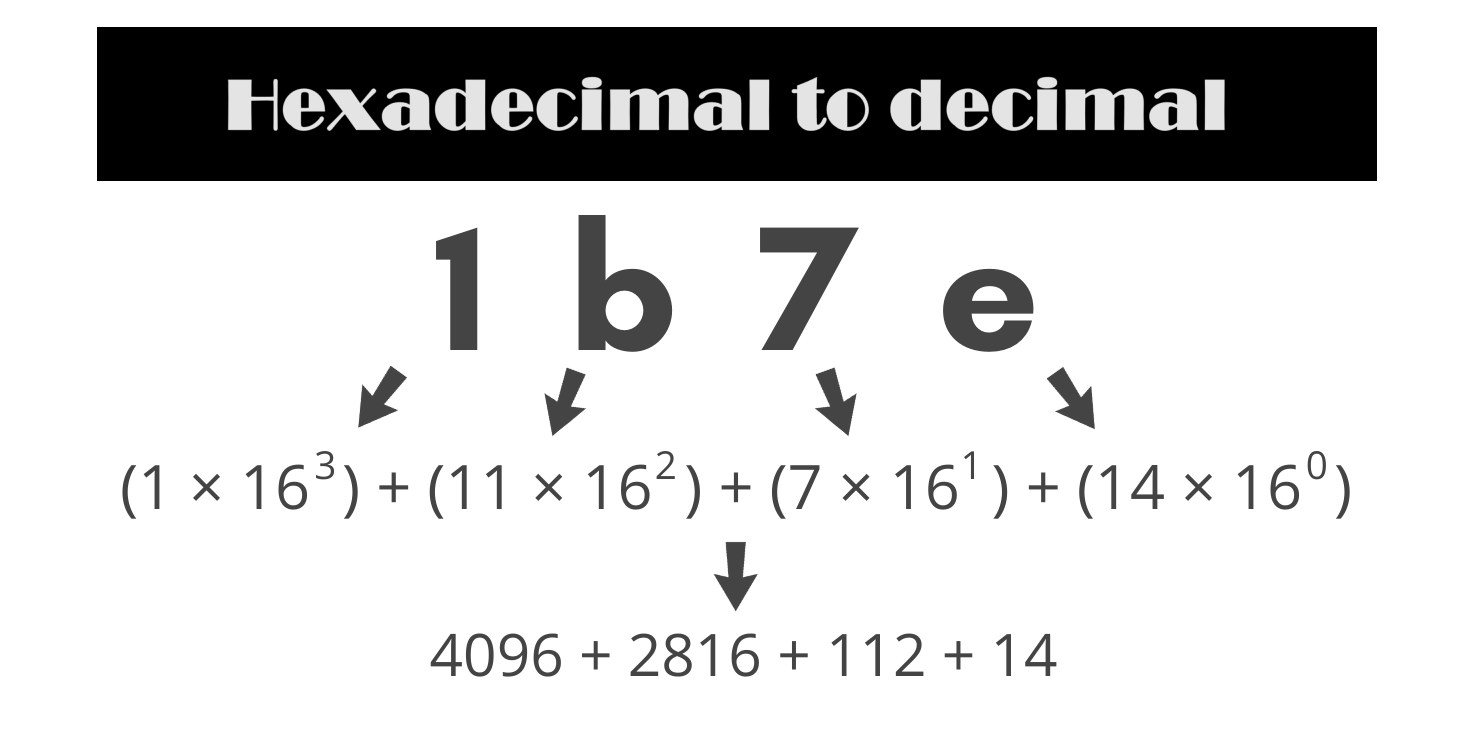
An example of hexadecimal to decimal conversion:
(A7.62)16 = (?)10 or make a conversion binary to decimal.
| Hexadecimal number: | A | 7 | . | 6 | 2 |
|---|---|---|---|---|---|
| power of 16: | 161 | 160 | . | 16-1 | 16-2 |
(A7.62)16 = (?)10
= 10 x 161 + 7 x 160 + 6 x 16-1 + 2 x 16-2
= 40 + 7 + 0.75 + 0.03125
= (47.78125)10
Hexadecimal to decimal conversion table:
| Hexadecimal | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
| 10 | 16 |
| 11 | 17 |
| 12 | 18 |
| 13 | 19 |
| 14 | 20 |