Binary To Decimal Converter
2
10
How to convert a binary number to a decimal number?
Converting a binary number to a decimal number involves multiplying each binary digit by the corresponding power of 2 and summing up the results, to more precise we need to Digit * 2 digit position. See the example below how position is calculated:
| Binary Number: | 1 | 0 | 1 | 1 | . | 1 | 0 |
|---|---|---|---|---|---|---|---|
| Position of Digit: | 3 | 2 | 1 | 0 | . | -1 | -2 |
| Digit * power of 2: | 1*23 | 0*22 | 1*21 | 1*20 | . | 1*2−1 | 0*2−2 |
Imagin a number is: dn-1 .... d4 d3 d3 d2 d1 d0
The decimal number is equal to the sum of binary digits (dn) times their power of 2 (2n), which is the base of binary number system:
decimal = dn-1 x 2n-1 + .... + d1 x 21 + d0 x 20 + d-1 x 2-1 + .... + d-n x 2-n
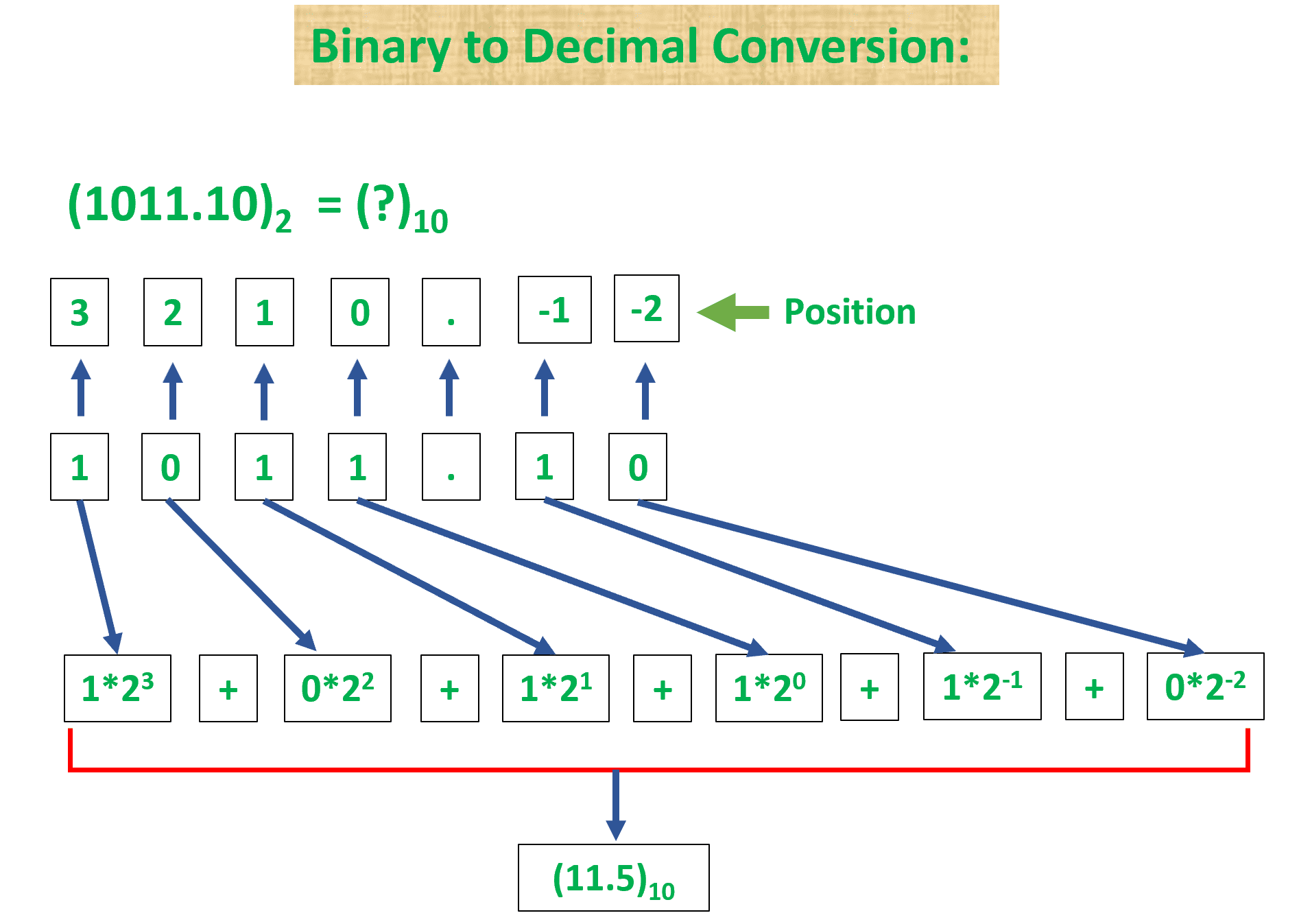
An example of binary to decimal conversion.
(1011.10)2 = (?)10 or make a conversion binary to decimal.
| binary number: | 1 | 0 | 1 | 1 | . | 1 | 0 |
|---|---|---|---|---|---|---|---|
| power of 2: | 23 | 22 | 21 | 20 | . | 2−1 | 2−2 |
=(1011.10)2
= 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 + 1 x 2-1 + 0 x 2-2
= 8 + 0 + 2 + 1 + .5 + 0
= (11.5)10
Binary to decimal conversion table
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |