Octal To Binary Converter
Calculation steps of octal to binary:
How to convert a octal number to the binary?
Converting an octal number to binary involves a systematic process where each digit in the octal number is replaced with its corresponding binary representation. In octal, each digit represents a power of 8, and in binary, each digit represents a power of 2. To perform the conversion, a table is utilized, mapping each octal digit to its binary equivalent. Starting from the leftmost digit of the octal number, each digit is substituted with its binary counterpart, ensuring that the binary representation is three bits long by adding leading zeros if needed. The binary representations of individual octal digits are then combined to yield the binary equivalent of the entire octal number. The final result may be further refined by removing any leading zeros. This method offers a step-by-step approach to manually convert octal numbers to binary, providing a clear understanding of the positional values and binary representations associated with each octal digit.
Converting octal to binary is also super easy. As we know base of octal is 8 and base of binary is 2, so we can make a relation between binary base and octal base and that is
2 ⇔23⇔ 8. Now we can clearly understand if we transform one octal into to three binary digit together it will be a binary number.
[N:B: We can remove the extra zeros as like given in the example below:]
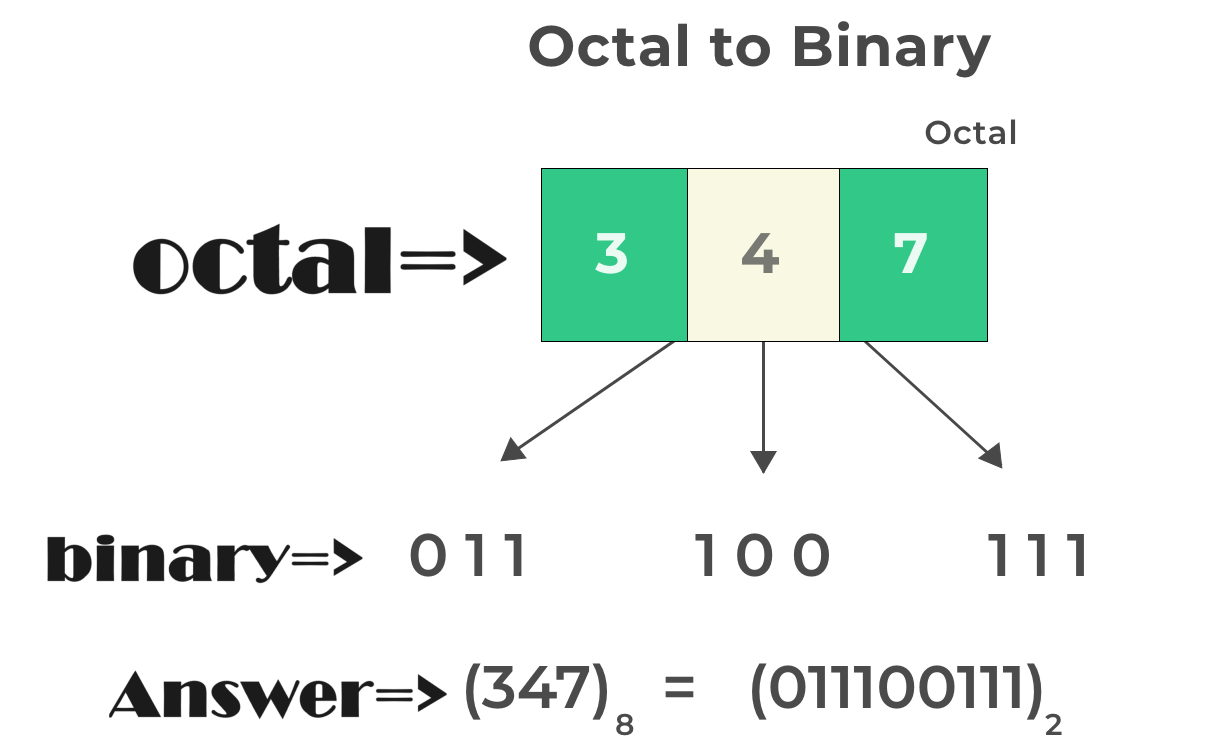
Example of octal to binary conversion:
(217.102)8 = (?)2
| Octal= | 2 | 1 | 7 | . | 1 | 0 | 2 |
|---|---|---|---|---|---|---|---|
| Arrow= | ↓ | ↓ | ↓ | . | ↓ | ↓ | ↓ |
| Chunk= | ______ | ______ | ______ | . | ______ | ______ | ______ |
| Binary= | 0 1 0 | 0 0 1 | 1 1 1 | . | 0 0 1 | 0 0 0 | 0 1 0 |
Result is = (010001111.001000010)2 or (10001111.00100001)2
Octal to binary conversion table:
| Octal | Binary |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 10 | 001000 |
| 11 | 001001 |
| 12 | 001010 |
| 13 | 001011 |
| 14 | 001100 |
| 15 | 001101 |