Octal To Decimal Converter

From

Enter Octal Number

₈

Result

₁₀

How to convert a octal number to the decimal number?

Converting an octal number to decimal is a straightforward process where each octal digit is treated as a positional value in base-8 and then summed up. In octal, each digit represents powers of 8. Begin by understanding the positional values of each digit, with the rightmost digit representing 8⁰, the next 8¹, and so on. Replace each octal digit with its decimal equivalent: Convert each octal digit to its decimal equivalent and multiply it by the corresponding positional value. Sum up these products to obtain the decimal equivalent of the entire octal number. This method provides a clear step-by-step approach for manual conversion, allowing for a better understanding of the positional values associated with each octal digit.

For d number of octal digit.[where n = 1,2,3... is positon of that digit.]:

d_n-1 .... d₄ d₃ d₃ d₂ d₁ d₀ . d_-1 d_-2 d_-3

The decimal number is equal to the sum of octal digits (d_n) times their power of (8ⁿ):

decimal = d_n-1 x 8^n-1 + .... + d₁ x 8¹ + d₀ x 8⁰ + d_-1 x 8^-1 + .... + d_-n x 8^-n

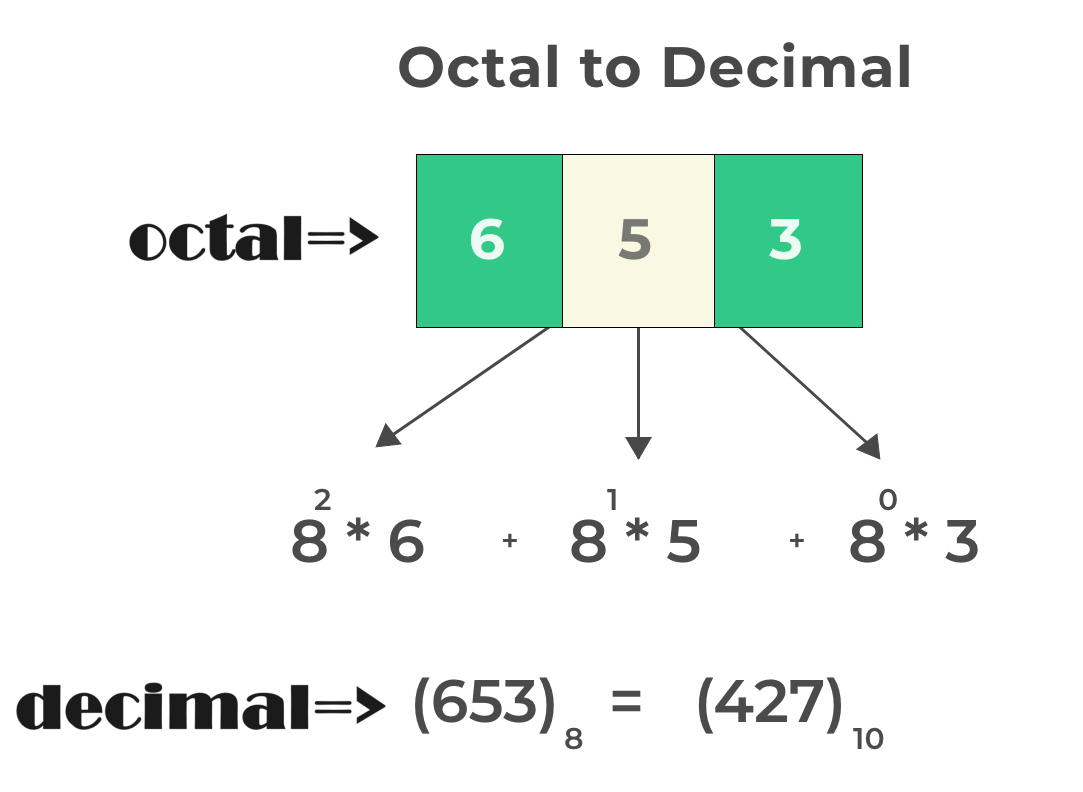
Example of octal to decimal conversion.

(57.62)₈ = (?)₁₀ or make a conversion binary to decimal.

octal number:	5	7	.	6	2
power of 8:	8¹	8⁰		8^-1	8^-2

(57.62)₈= (?) ₁₀
= 5 x 8¹ + 7 x 8⁰ + 6 x 8^-1 + 2 x 8^-2
= 40 + 7 + 0.75 + 0.03125
= (47.78125)₁₀

Binary to decimal conversion table:

Octal	Decimal
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
10	8
11	9
12	10
13	11
14	12
15	13
16	14
17	15
20	16
21	17
22	18
23	19
24	20

Octal	Decimal
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
10	8
11	9
12	10
13	11
14	12
15	13
16	14
17	15
20	16
21	17
22	18
23	19
24	20

Octal	Decimal
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
10	8
11	9
12	10
13	11
14	12
15	13
16	14
17	15
20	16
21	17
22	18
23	19
24	20

Octal	Decimal
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
10	8
11	9
12	10
13	11
14	12
15	13
16	14
17	15
20	16
21	17
22	18
23	19
24	20